In July of 1887, Carl Benz held the first public outing for his “vehicle powered by a gas engine” – the first automobile ever invented. Nine short months after the first car was publicly displayed, the first auto race was staged on April 28, 1887 and spanned a distance of 2 kilometres (1.2 mi) from Neuilly Bridge to the Bois de Boulogne in Paris.
As cars became more dependable and commonplace as a means of convenient transportation, so too grew the desire to discover the technology’s potential. Auto racing formally became an organized sport in the early 1900’s and today it’s a multi-billion dollar per year industry and has produced vehicles capable of max speeds of almost 500kph (over 300mph).
Similar to that first auto race, Artificial Intelligence (AI) applications are in their nascent years, but many are speculating that their impact may be even greater than that of the automobile and many are racing to test their current limits. Similar to how race cars today look nothing like the original three-wheeled Motor Car, AI platforms are changing to meet the performance demands of this new class of programs.
If you’ve been following any of the companies that are joining this race, you may have heard them use the term “operator fusion“ when bragging about their AI acceleration capabilities. One of the most brag-worthy features to come out of the PyTorch 2.0. release earlier this year was the ‘TorchInductor’ compiler backend that can automatically perform operator fusion, which resulted in 30-200% runtime performance improvements for some users.
From context, you can probably infer that “operator fusion“ is some technique that magically makes Deep Neural Network (DNN) models easier and faster to execute… and you wouldn’t be wrong. But what exactly is operator fusion and how can I use operator fusion to accelerate my AI inference applications?
AI applications, especially those that incorporate Deep Neural Network (DNN) inference, are composed of many fundamental operations such as Multiply-Accumulate (MAC), Pooling layers, activation functions, etc.
Conceptually, operator fusion (sometimes also referred to as kernel or layer fusion) is an optimization technique for reducing the costs of two or more operators in succession by reconsidering their scope as if they were a single operator.
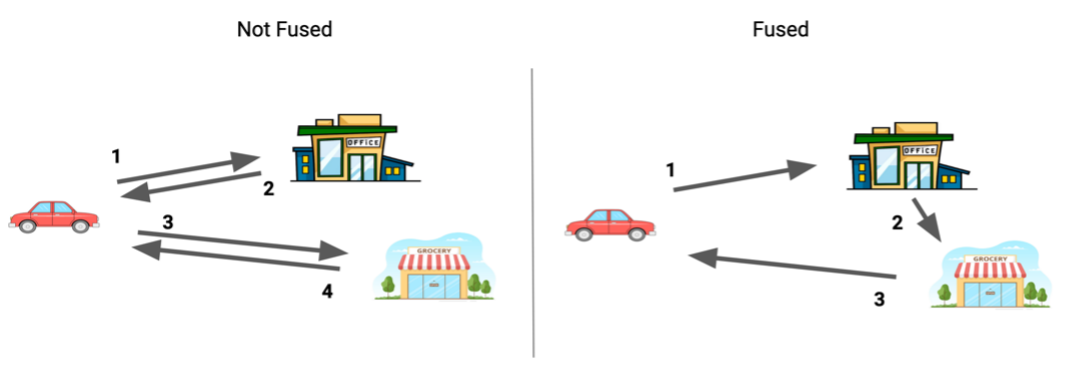
You intuitively do this type of “fusion“ routinely in your everyday life without much thought. Consider for example that you have two tasks in a given day: going to the office for work and going to the grocery store for this week's groceries.
Figure 1. Reducing instances of driving by one by fusing two tasks – “going to work“ and “going to the grocery store“ – by reconsidering them as a single task. Image by Author.
If your office and local grocery store are in the same part of town, you might instinctively stop by the grocery store on your way home from work, reducing the number of legs of your journey by 1 which might result in less total time spent driving and less total distance driven.
Operator fusion intuitively optimizes AI programs in a similar way, but the performance benefits are measured in fewer memory read/writes which results in fewer clock cycles dedicated to program overhead which generates a more efficient program binary.
Let’s look at a practical example. Here’s a visual diagram of a network before and after operator fusion performed by NVIDIA’s TensorRT™ Optimizer:
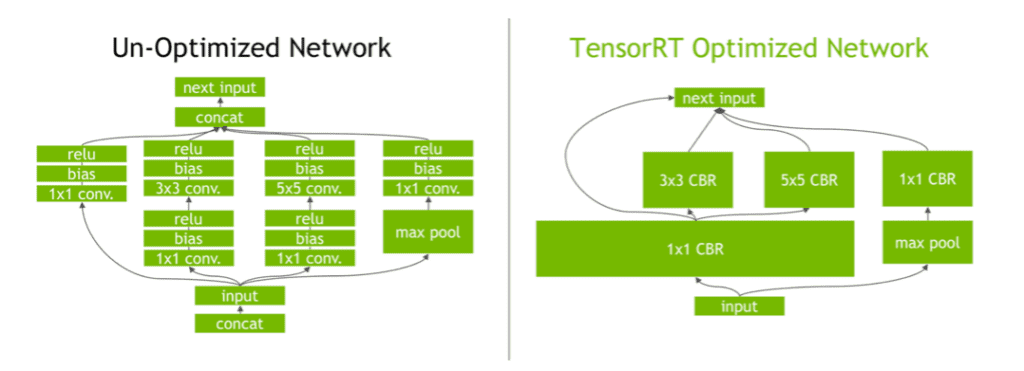
Figure 2. A GoogLeNet Inception module network before and after layer fusion performed by NVIDIA’s TensorRT™ Optimizer. Original image available in this blog post by NVIDIA.
In the example in Figure 2, operator fusion was able to reduce the number of layers (blocks not named “input“ or “next input“) from 20 to 5 by fusing combinations of the following operators:
The performance benefits vary depending on the hardware platform being targeted, but operator fusion can provide benefits for nearly every runtime target. Because of its universality, operator fusion is a key optimization technique in nearly all DNN compilers and execution frameworks.
If reducing the number of kernels reduces program overhead and improves efficiency and these benefits are applicable universally, this might lead us to ask questions like:
To better understand operator fusion's benefits and limitations, let’s take a deeper dive into the problem it’s solving.
Fusing convolutional layers, bias adds, and activation function layers, like NVIDIA’s TensorRT tool did in Figure 2, is an extremely common choice for operator fusion. Convolutions and activation functions can be decomposed into a series of matrix multiplication operations followed by element-wise operations that look something like:
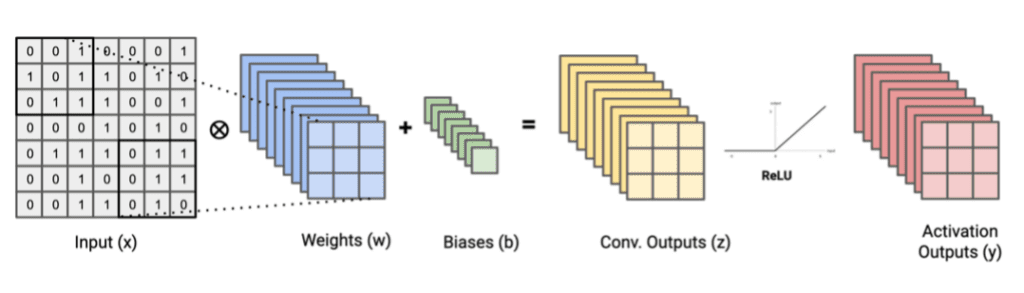
Figure 3. Tensors used in a 3x3 Conv., Bias Add, and ReLU activation function sequence of graph operators. Image by Author.
If these operations are performed in three sequential steps, the graph computation would look something like (left side of Figure 4):
Activation outputs (y) are written to global memory to be used by next operator(s) in the graph
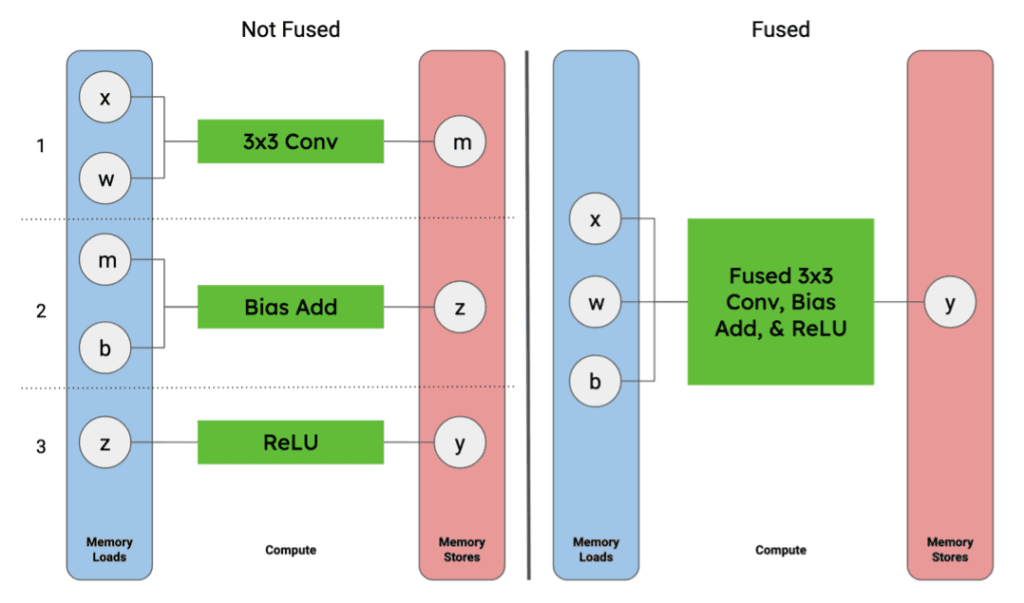
Figure 4. Local memory loads and stores for tensors used in a 3x3 Conv., Bias Add, and ReLU activation function sequence of graph operators compared to a single fused operator. Image by Author.
If the two operations are fused, the graph computation becomes simplified to something like (right side of Figure 4):
By representing these three operations as a single operation, we are able to remove four steps:the need to write and read the intermediate tensor (m) and the convolution output tensor (z) out of and back into local memory. In practice, operator fusion is typically achieved when a platform can keep intermediate tensors in local memory on the accelerator platform.
There are three things that dictate whether the intermediate tensors can remain in local memory:
As we mentioned before, some accelerator platforms are better suited to capitalize on the performance benefits of operator fusion than others. In the next section, we’ll explore why some architectures are more equipped to satisfy these requirements.
DNN models are becoming increasingly deep with hundreds or even thousands of operator layers in order to achieve higher accuracy when solving problems with increasingly broader scopes. As DNNs get bigger and deeper, the memory and computational requirements for running inference also increase.
There are numerous hardware platforms that optimize performance for these compute and memory bottlenecks in a number of clever ways. The benefits of each can be highly subjective to the program(s) being deployed.
We’re going to look at three different types of accelerator cores that can be coupled with a host CPU on a System-on-Chip (SoC) and be targeted for
and see how capable each architecture is of operator fusion:
GPUs, like the Arm Mali-G720, address the memory bottlenecks of AI and abstract the programming complexity of managing memory by using L2 cache. They address the compute bottlenecks by being comprised of general compute cores that operate in parallel, but cannot communicate directly with one another.
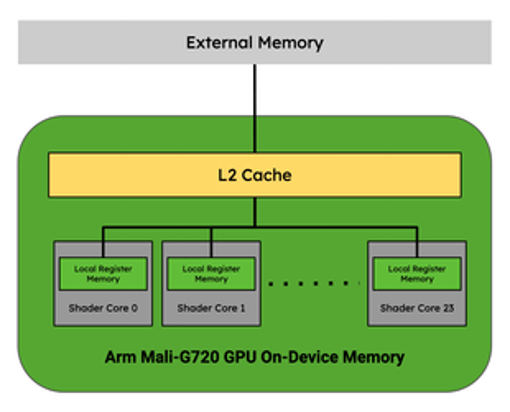
Figure 5. Arm Mali-G720 GPU Memory Hierarchy. Adapted from a diagram in this blog post
In the context of a GPU’s memory hierarchy, operator fusion is possible if the intermediate tensors can fit entirely in the Local Register Memory (LRM) of a given Shader Core without needing to communicate back out to L2 cache.
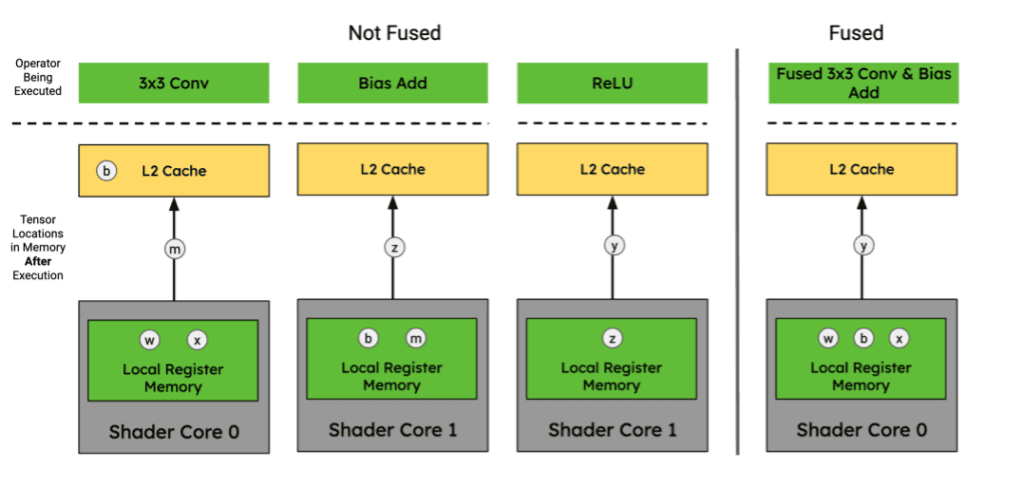
Figure 6. Tensor locations for 3x3 Conv., Bias Add, and ReLU activation function sequence of graph operators in an Arm Mali-G720 GPU memory hierarchy. Image by Author.
Since the GPU cores cannot share data directly with one another, they must write back to L2 Cache in order to exchange intermediate tensor data between processing elements or reorganize to satisfy the requirements of the subsequent operators. This inability to share tensor data between compute cores without writing to and from L2 cache prevents them from fusing multiple convolutions together without duplicating weight tensors across cores which taxes their compute efficiency and memory utilization. Since the memory hierarchy is cache-based, the hardware determines when blocks of memory are evicted or not which can make operator fusion nondeterministic if the available memory is approaching saturation.
For these reasons, GPUs satisfy the compute generality requirement for operator fusion, but are occasionally vulnerable to the memory availability and memory organization requirements.
NPUs, like the Arm Ethos-N78, are customized hardware-accelerator architectures for accelerating AI and, therefore, the way they accelerate AI varies; however the most performant ones today typically use hard-wired systolic arrays to accelerate MAC operations.
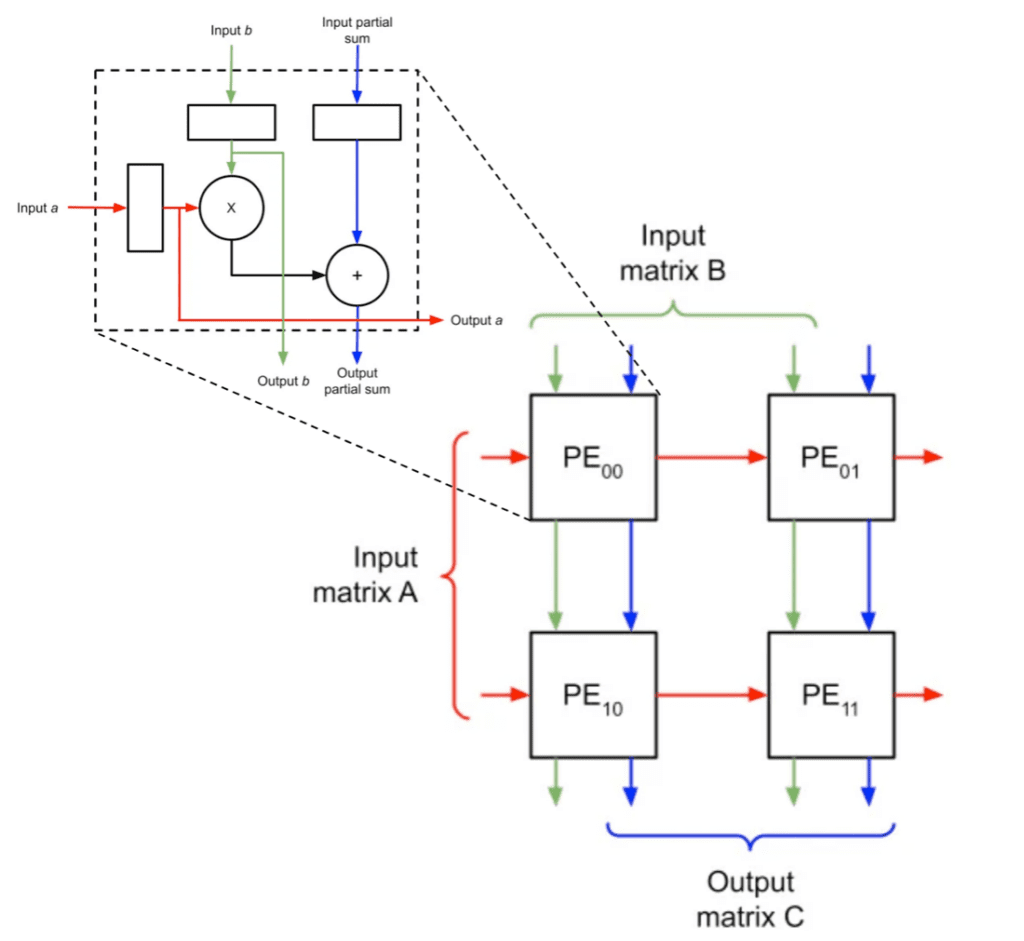
Figure 7. Diagram of a systolic array for MAC operations. Original image adapted from two images in this blog post.
MAC operations are the most frequent and, therefore, are often the most expensive operations found in DNN inference. Since NPUs that use systolic arrays are designed to accelerate this compute, they are ultra-efficient and high-performance for 90%+ of the compute needed to run DNN inference and can be the logical choice for some AI applications.
Although NPUs are extremely performant for MAC operations, they’re not capable of handling all operators and most be coupled with a more general processing element to run an entire program. Some NPUs will off-load this compute to the host CPU. The more performant ones have dedicated hardware blocks next to the systolic arrays to perform limited operator fusion for things like bias adds and activation functions.
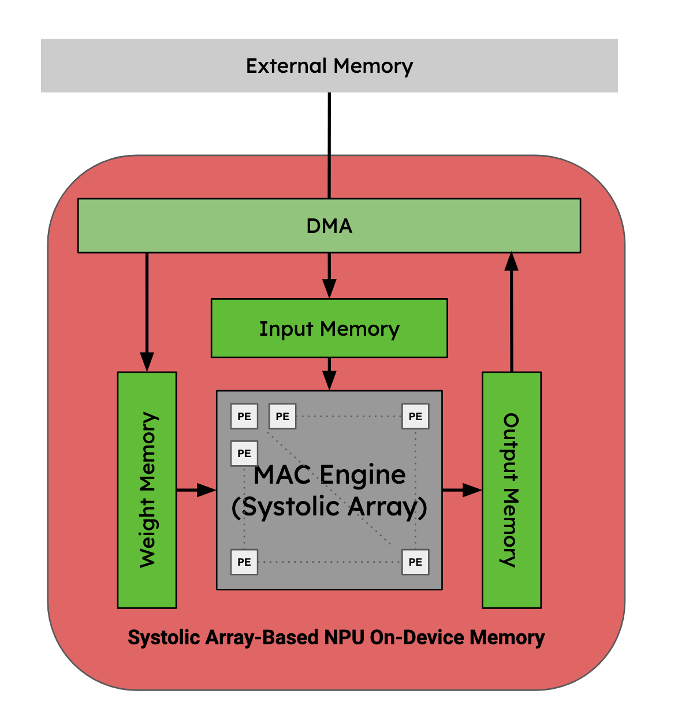
Figure 8. Memory hierarchy for a MAC acceleration systolic array NPU. Image by Author.
In the context of an ASIC’s memory hierarchy, operator fusion is possible if the intermediate tensors can continuously flow through the systolic array and on-chip processing elements without needing to communicate back to the host’s shared memory.
The most performant NPU’s are designed with operator fusion in mind for a limited set of permutations of operators. Since they are hard-wired and therefore cannot be programmed, they cannot handle memory reshaping or reorganization or even fuse some activation functions that aren’t handled by their coupled hardware blocks. To perform these operations, the programs must write back out to some shared memory: either on device or shared memory on the SoC.
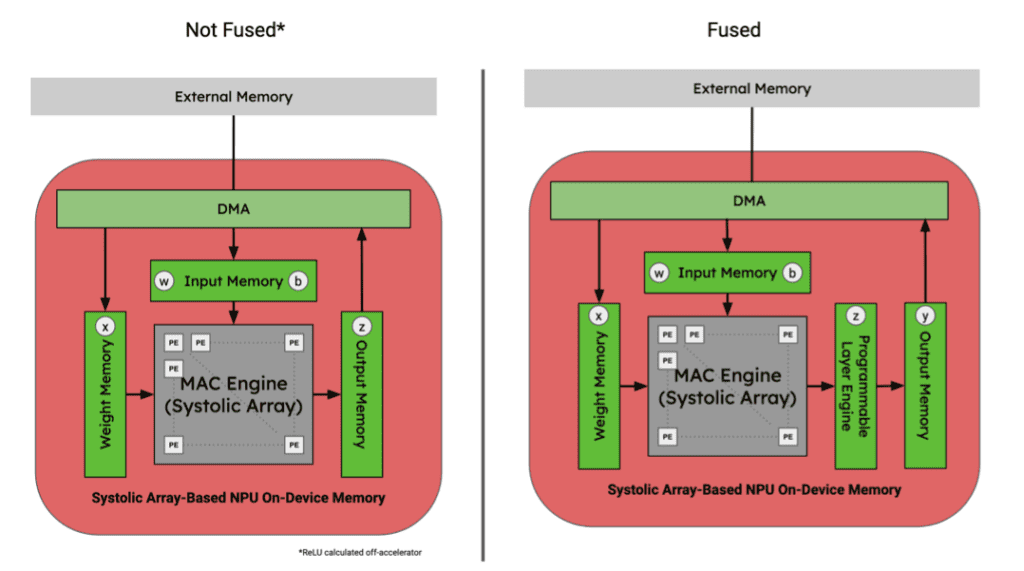
Figure 9. Tensor locations for 3x3 Conv., Bias Add, and ReLU activation function sequence of graph operators in an NPU memory hierarchy. Image by Author.
Their lack of programmability and sensitivity to some model architectures, like the increasingly popular transformers, make them inaccessible to many AI applications. Shameless plug: if you’re interested in learning more about this subject, check out our recent blog post on this topic.
For these reasons, custom NPU accelerators do not satisfy the compute generality and memory organization requirements for broadly-applicable operator fusion.
GPNPUs, like the Quadric Chimera QB16 processor, are also purpose-built processor architectures and, therefore, the way they accelerate AI varies; however, most use distributed compute elements in a mesh network for parallelization of compute and more efficient memory management.
GPNPUs strike a middle ground between NPUs and GPUs by being capable of both AI application-specific and generally programmable. Using thoughtful hardware-software co-design, they’re able to reduce the amount of hardware resources consumed while also being fully programmable.
The Chimera family of GPNPUs are fully C++ programmable processor cores containing a networked mesh of Processing Elements (PEs) within the context of a single-issue, in-order processor pipeline. Each PE has its own local register memory (LRM) and collectively are capable of running scalar, vector, and matrix operations in parallel. They’re mesh-connected thus are capable of sharing intermediate tensor data directly with neighboring PEs without writing to shared L2 memory.
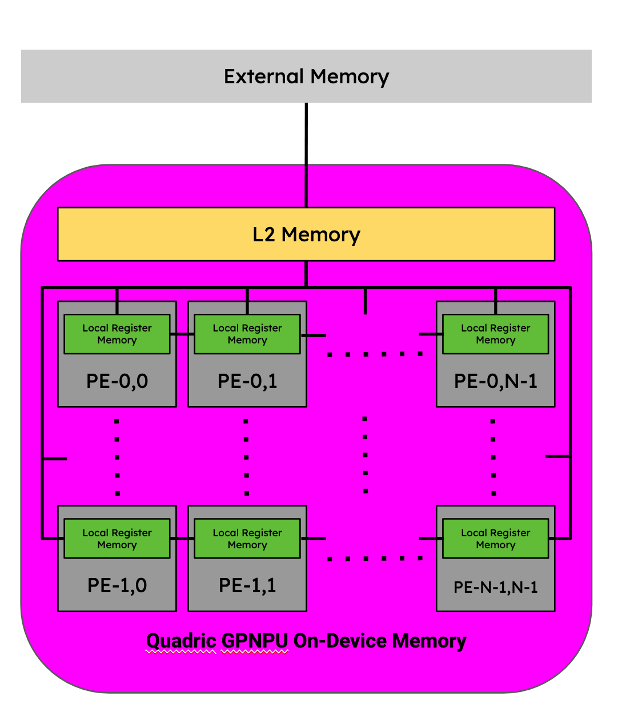
Figure 10. Memory hierarchy for a Quadric GPNPU. Image by Author.
In the context of a GPNPU's memory hierarchy, two successive operations are considered to be fused if the intermediate tensor(s) between those two operations do not leave the distributed LRM, the memory block within each PE.
The difference between the PEs in a systolic array and the array of PEs in the GPNPU is that the PEs are collectively programmed to operate in parallel using the same instruction stream. Since the dataflow of most DNN operators can be statically defined using access patterns, simple APIs can be written to describe the distribution and flow of the data through the array of PEs. This greatly simplifies the developer experience because complex algorithms can be written without needing to explicitly program every internal DMA transfer. In the instance of Quadric’s Chimera processor, the Chimera Compute Library (CCL) provides all of those higher-level APIs to abstract the data movement such that the programmer does not need to explicitly gain deep knowledge of the two-level DMA within the architecture.
For these reasons, GPNPUs strike a balance between thoughtfully designed hardware for AI compute with the programmability and flexibility of a general-parallel compute platform like a GPU. GPNPUs satisfy the general compute and the memory organization requirements for operator fusion and are only limited occasionally by the memory availability requirement.
Let’s take a look at a similar practical example of operator fusion performed by a GPNPU and its compiler, the Chimera Graph Compiler (CGC).
Here’s a visual diagram of a MobileNetV2 network before and after operator fusion performed by Quadric’s Chimera™ Graph Compiler (CGC) in the style of NVIDIA’s diagram from Figure 2:
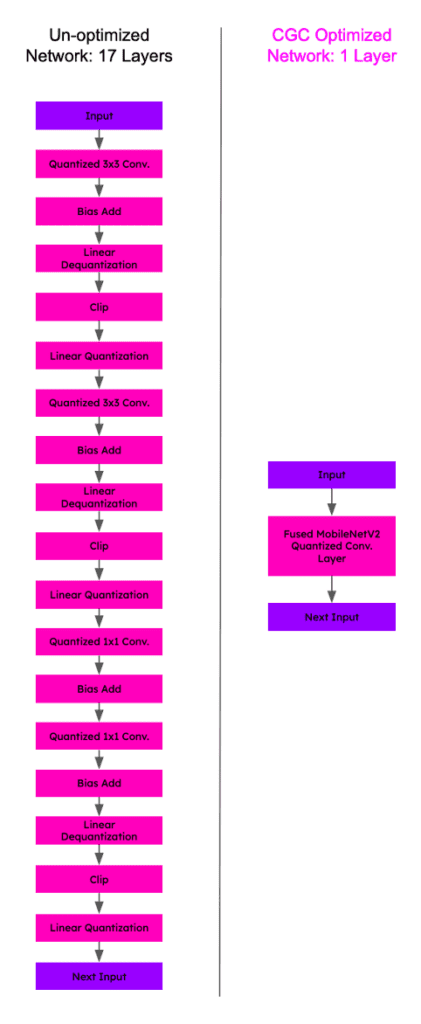
Figure 11. A MobileNetV2 module network before and after layer operator fusion performed by Quadric’s Chimera™ Graph Compiler (CGC).
In the example above, operator fusion performed by CGC was able to reduce the number of layers from 17 to 1. This feat is even more impressive when you consider the sequence of layers that were fused.
The fused layer produced by CGC contains four convolutional operators with varying number of channels and filter sizes. Since the GPNPU uses a networked mesh of PEs, data can be shared by neighboring PEs without writing back out to shared L2 memory. These data movements are an order of magnitude faster than writing out to L2 memory and allow data to “flow” through the PEs similar to how a systolic array computes MAC operations, but in a programmable way.
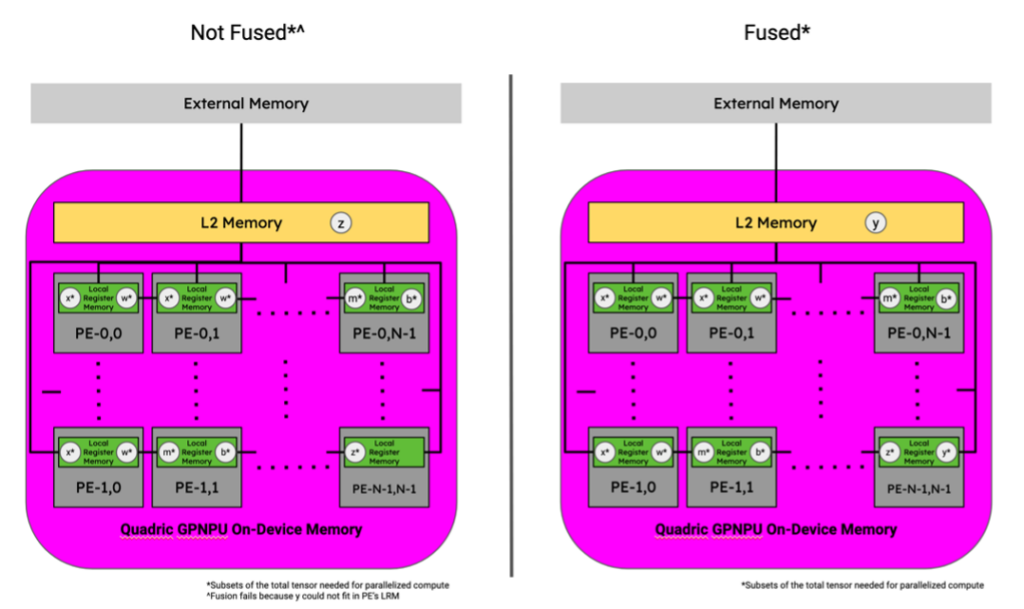
Figure 12. Tensor locations for 3x3 Conv., Bias Add, and ReLU activation function sequence of graph operators in an Quadric Chimera GPNPU memory hierarchy. Image by Author.
Since the PEs are collectively programmed with a single instruction stream, the APIs available to represent these operators are remarkably simple which can result in very short, but performant code. Below is the auto-generated C++ code-snippet for the MobileNetV2 operators from Figure 10 generated by Quadric’s CGC. Without comments, which have been added, it is 37 lines of code for all 17 operators:
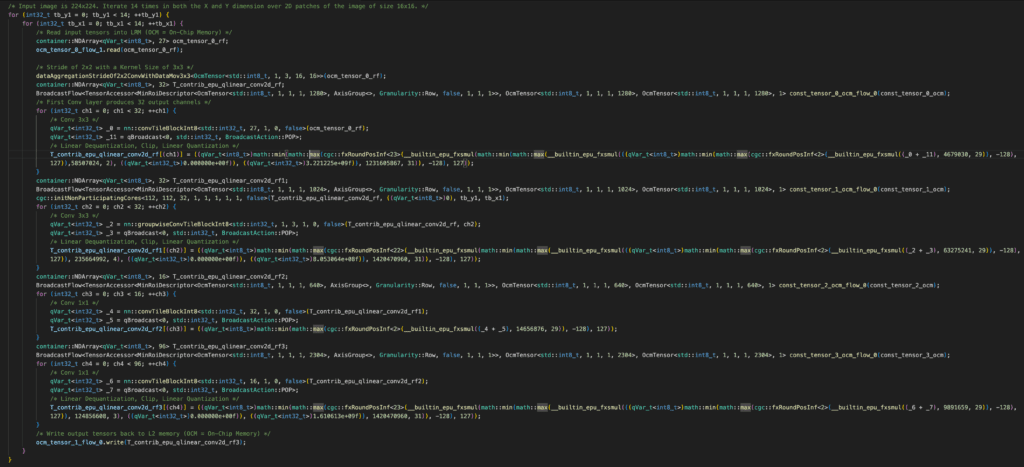
The total size of the intermediate tensors that were fused in this code snippet and therefore not moved between LRM and L2 memory was 6,623.2 KB or ~6.6 MB. For context, the input data passed into the first layer of this block was 150.5 KB and the intermediate tensor data that was finally moved out to L2 memory was 1.2 MB. By aggressively leveraging operator fusion, CGC was able to reduce the total memory movement overhead of this section of the MobileNetV2 kernel by 83%.
For high-performance edge applications that are optimizing performance for TOPS/W, these data movement savings translate directly to power savings. Below in Figure 13 is a table of the relative costs associated with moving a 32b data element from the ALU/MAC engine register file memory on a Chimera GPNPU to each of the other levels of memory:
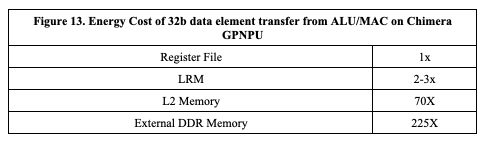
By performing operator fusion and not moving those 6.6 MB of intermediate tensor data, an application developer can expect a ~185x reduction in power consumption.
If you’re a hardware designer looking to enable high-performance, lower power AI applications for your developers and are interested in the potential performance benefits that Quadric’s Chimera Graph Compiler (CGC) can provide, consider signing up for a Quadric DevStudio account to learn more.